Question

Determine
a piecewise equation for the function shown graphed below.

Answer 1

f(x)=
`\left \{ {{x-4, -5\leq x < -1} \atop {2x+6, -1\leq x\leq 4}} \atop {(1)/(2) x}+5, 4 < x\leq 8}} \right.`

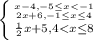
Explanation:

x-4, -5≤x<-1: the slope of the first line goes up once and to the right once and so is 1. If you follow the pattern, the y-intercept would be -4 so x-4 is the equation of the line. The endpoint at -5 is a closed circle so it is included while the endpoint at -1 is an open circle so it is not included (not equal to in the domain).

2x+6, -1≤x ≤4: the slope of the line is determined as rise over run and it goes up twice every 1 unit right so the slope is 2. The line crosses over the y-intercept at 6 so when plugged into slope-intercept form mx+b, it would be 2x+6. Both endpoints are closed circles so -1 and 4 are added into the domain(have equal to in the inequality).

1/2x+5, 4<x≤8: the slope is 1/2 as it goes up once every 2 units right. The line would cross over at 5 if you follow the slope past the y-axis. so the equation is 1/2x+5. The end point at 4 is an open circle so it is not included and is not equal to only greater than. On the other hand, the endpoint at 8 is a closed circle so it is equal to and less than.