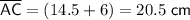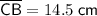Question

Point C belongs to segment AB and segment AB= 35 cm. The distance from C to A is 6 cm longer than the distance from C to B. Find AC and CB.

Answer 1

Answer: AC = 20.5 cm CB = 14.5 cm

Explanation:

Since we know that segment AC is 6 cm longer than CB, we can can substitute AC as CB + 6.

CB = CB

AC = CB + 6

We know that AB is 35 cm, and AB is made up of AC and CB, so we now have the equation CB + CB + 6 = 35

Now, we solve.

CB + CB + 6 = 35

2CB = 29

CB = 29/2

CB = 14.5 cm

AC = CB + 6 = 14.5 + 6 = 20.5 cm

Answer 2

AC = 20.5 cm

CB = 14.5 cm

Explanation:

Let x be the distance from point C to point B:

`\overline{\sf CB} = x \;\sf cm`

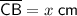
Given that the distance from A to C is 6 cm longer than the distance from C to B, then:

`\overline{\sf AC} = (x + 6) \;\sf cm`

Now, we know that segment AB is 35 cm long, and it can be expressed as the sum of AC and CB, so:

`\overline{\sf AC}+\overline{\sf CB}=\overline{\sf AB}`

`x+6+x=35`

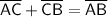
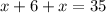
Solve for x:

`\begin{aligned}2x+6&=35\\\\2x+6-6&=35-6\\\\2x&=29\\\\(2x)/(2)&=(29)/(2)\\\\x&=14.5\; \sf cm\end{aligned}`

So, the lengths of the two line segments are:

`\overline{\sf AC} = (14.5 + 6)=20.5 \;\sf cm`

`\overline{\sf CB} = 14.5 \;\sf cm`