Answer:
Hi,
12th term.
Explanation:
The given sequence is an arithmetic sequence with a common difference of 3.
We can find the term using the formula for the nth term of an arithmetic sequence:
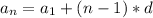
where:
 is the nth term of the sequence
is the nth term of the sequence
 is the first term
is the first term
d is the common difference between the terms
n is the term number we want to find
Here, we have:
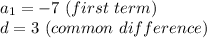
We want to find the term where
 .
.
Let's substitute these values into the formula and solve for n:
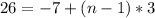

So, the 12th term of the sequence is 26.