Question

a bank pays 3% compound interest. jenna invests 410 dollars for the past 5 years, how much is in the account after 5 years

Answer 1

$475.30

Explanation:

To calculate the future value of an investment with compound interest, we can use the compound interest formula:

`\sf A = P \left(1 + (r)/(n)\right)^(nt)`

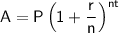
Where:

• A is the ending amount
• P is the principal amount (the initial investment)
• r is the annual interest rate
• n is the number of times the interest is compounded per year
• t is the number of years

In this case, we have:

• P = $410
• r = 3%
• n = 1 (compounded annually)
• t = 5 years

Substitute these values into the formula and simplify:

`\begin{aligned} \textsf{ Ending Amount (A)} &= 410 \left(1 + (0.03)/(1)\right)^(1 \cdot 5) \\\\ & = 410 \left(1 + 0.03\right)^5 \\\\ & = 410 \cdot 1.03^5 \\\\ & = 410 \cdot 1.1592740740743 \\\\ & = 475.302370463 \\\\ &= 475.30 \textsf{(in 2 d.p)} \end{aligned}`

Therefore, Jenna will have $475.30 in her account after 5 years.