Question

A lighter block (2 kg) and a heavier block (8 kg) sit on a frictionless surface. Both blocks are initially at rest. The same force of 4 N then pushes to the right on each block for a distance of 1 m

What are the changes in kinetic energy of the blocks? What are the final kinetic energies of the blocks? What are the initial momenta of the blocks?
What are the final momenta of the blocks?

Answer 1

The lighter block gained
`0.8\; {\rm J}` of kinetic energy. The heavier block gained
`3.2\; {\rm J}` of kinetic energy.

Final kinetic energy:
`0.8\; {\rm J}` for the lighter block, and
`3.2\; {\rm J}` for the heavier block.

Initial momenta of both blocks were
`0\; {\rm kg\cdot m\cdot s^(-1)}`.

Final momentum: approximately
`1.79\; {\rm kg \cdot m\cdot s^(-1)}` for the lighter block, and approximately
`7.16\; {\rm kg \cdot m\cdot s^(-1)}` for the heavier block.

(Assumption: the surface is level.)

Step-by-step explanation:

Since the two blocks are moving together, their acceleration and velocity would be the same throughout the motion.

Approach this question in the following steps:

• With the two blocks considered as one object, determine the acceleration of this object. This acceleration is the same for both blocks.
• Apply SUVAT equations to find the final velocity of both blocks.
• Find the kinetic energies and momenta of the two blocks separately before and after the acceleration.

Since the two blocks as moving together, they can be considered as one object when calculating acceleration. The mass of this combined object is
`(2\; {\rm kg} + 8\; {\rm kg})`. Assuming that the surface is level, the net force on this object would be equal to the external force, such that
`F_{\text{net}} = 4\; {\rm N}`.

Hence, the acceleration of this combined object would be:

`\begin{aligned}a &= \frac{F_{\text{net}}}{m} \\ &= \frac{4\; {\rm N}}{2\; {\rm kg} + 8\; {\rm kg}} = (2)/(5)\; {\rm m\cdot s^(-2)}\end{aligned}`.

Because the two blocks are moving together, the acceleration of each block would be equal to the acceleration of this combined object:
`(2/5)\; {\rm m\cdot s^(-2)}`.

Since acceleration is constant, it would be possible to find the final velocity using the SUVAT equations. Because the two blocks are travelling at the same velocity, the final velocity of the two blocks would also be the same.

In this question, initial velocity
`u`, acceleration
`a`, and displacement
`x` are all known. The final velocity
`v` can be found with the following equation:

`v^(2) - u^(2) = 2\, a\, x`,

Where:

• 
  `v` is the final velocity that needs to be found,
• 
  `u = 0\; {\rm m\cdot s^(-1)}` because this combined object was initially not moving,
• 
  `a = (2/5)\; {\rm m\cdot s^(-2)}` from previous calculations, and
• 
  `x = 1\; {\rm m}`.

Rearrange the SUVAT equation
`v^(2) - u^(2) = 2\, a\, x` to find
`v`:

`\begin{aligned}v &= \sqrt{u^(2) + 2\, a\, x} \\ &= \sqrt{0^(2) + 2\, (2/5)\, (1)}\; {\rm m\cdot s^(-1)} \\ &\approx (2)/(√(5))\; {\rm m\cdot s^(-1)}\end{aligned}`.

In other words, the final velocity of both blocks would be
`\left(2/√(5)\right) \; {\rm m\cdot s^(-1)}`.

When an object of mass
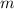`m` travels at a speed of
`v`, the kinetic energy of that object would be
`(1/2)\, m\, v^(2)`.

The kinetic energy of both blocks was initial
`0\; {\rm J}` because both blocks were initially stationary (speed was
`0\; {\rm m\cdot s^(-1)}`.)

At the final speed of
`v = \left(2/√(5)\right) \; {\rm m\cdot s^(-1)}`, the kinetic energy of the two blocks would be:

• Lighter block:
  `(1/2)\, (2)\, \left(2 / √(5)\right)^(2)\; {\rm J} = 0.8\; {\rm J}`.
• Heavier block:
  `(1/2)\, (8)\, \left(2 / √(5)\right)^(2)\; {\rm J} = 3.2\; {\rm J}`.

Subtract the initial kinetic energy from the new value of kinetic energy to find the change:

• Lighter block:
  `0.8\; {\rm J} - 0\; {\rm J} = 0.8\; {\rm J}`.
• Heavier block:
  `3.2\; {\rm J} - 0\; {\rm J} = 3.2\; {\rm J}`.

When an object of mass
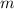`m` travels with a velocity of
`v`, the momentum of that object would be
`m\, v`.

Similarly, the initial momentum of both objects was
`0\; {\rm kg\cdot m\cdot s^(-1)}` because both objects were initially stationary (velocity was
`0\; {\rm m\cdot s^(-1)}`.)

At the final velocity of
`v = \left(2/√(5)\right) \; {\rm m\cdot s^(-1)}`, the momentum of the two blocks would be:

• Lighter block:
  `(2)\, \left(2 / √(5)\right)\; {\rm kg \cdot m\cdot s^(-1)} \approx 1.79\; {\rm kg \cdot m\cdot s^(-1)}`.
• Heavier block:
  `(8)\, \left(2 / √(5)\right)\; {\rm kg \cdot m\cdot s^(-1)} \approx 7.16\; {\rm kg \cdot m\cdot s^(-1)}`.