Question

Determine the value of x such that the area of the triangle shown is 66 square mm.

Answer 1

Answer: Approximately x = 9.257976 millimeters

Work Shown

area = 0.5*base*height

66 = 0.5*(x+5)*x

2*66 = x(x+5)

132 = x^2+5x

x^2+5x-132 = 0

Use the quadratic formula.

Plug in: a = 1, b = 5, c = -132.

`x = (-b\pm√(b^2-4ac))/(2a)\\\\x = (-5\pm√((5)^2-4(1)(-132)))/(2(1))\\\\x = (-5\pm√(553))/(2)\\\\x \approx (-5\pm23.515952)/(2)\\\\x \approx (-5+23.515952)/(2) \ \text{ or } \ x \approx (-5-23.515952)/(2)\\\\x \approx (18.515952)/(2) \ \text{ or } \ x \approx (-28.515952)/(2)\\\\x \approx 9.257976 \ \text{ or } \ x \approx -14.257976\\\\`

Ignore the negative x value. A negative side length is not possible.

Therefore, the value of x is roughly x = 9.257976

This is exactly equal to
`(-5+√(553))/(2)`

Meaning that
`(-5+√(553))/(2) \approx 9.257976`

I think a decimal value of x makes the most sense here. That way we can visualize how long each side of this triangle is.

Answer 2

`x=(-5+√(553))/(2)`

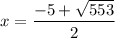
Explanation:

The area of a right triangle is half the product of its two legs,
`a` and
`b`:

`\boxed{\textsf{Area}=(1)/(2)ab}`

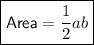
Given values:

• 
  `\textsf{Leg 1:}\quad a = x`
• 
  `\textsf{Leg 2:}\quad b = x + 5`
• 
  `\textsf{Area} = 66 \; \sf mm^2`

To determine the value of x, begin by substituting the values into the area formula:

`66=(1)/(2)\cdot x \cdot (x+5)`

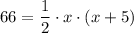
Multiply both sides of the equation by 2 to eliminate the fraction:

`132=x(x+5)`

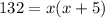
Expand the right side by multiplying x with each term inside the parentheses:

`132=x^2+5x`

Rearrange the equation into a quadratic equation, setting it equal to zero:

`x^2+5x-132=0`

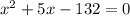
Now, solve this quadratic equation for x by using the quadratic formula:

`\boxed{\begin{array}{l}\underline{\sf Quadratic\;Formula}\\\\x=(-b \pm √(b^2-4ac))/(2a)\\\\\textsf{when} \;ax^2+bx+c=0 \\\end{array}}`

In this case:

• a = 1
• b = 5
• c = -132

Plug these values into the formula:

`x=(-(5) \pm √((5)^2-4(1)(-132)))/(2(1))`

Now, calculate the values of x:

`x=(-5\pm √(25+528))/(2)`

`x=(-5\pm √(553))/(2)`

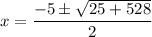
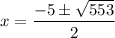
As length is positive, the only valid value of x is:

`\large\boxed{\boxed{x=(-5+√(553))/(2)}}`

`\hrulefill`

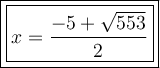
Additional Notes

The decimal value of x, rounded the nearest thousandth, is 9.258.