Question

Find the value of y in each equation.

1. 5^3x5^2y=125
2.2^3x2^y+3=8
3.27x3^y=3^2y
4.2^y-3x16=2^2y

Answer 1

Explanation:

1. The equation is :

`5^3*5^(2y) = 125`

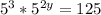
We know that 125=5^3, so we can rewrite the equation as:

`5^3*5^(2y) = 5^3`

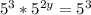
Since the bases are equal (base 5), the exponents must also be equal. Therefore, we have:

`3+2y=3\\`

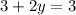
Subtracting 3 from both sides gives:

`2y = 0`

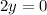
Finally, dividing both sides by 2 gives:

`y=0`

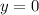
So, the value of y in the equation is 0.

2. The equation is:

`2^3*2^y+3=8`

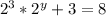
We know that 8=23, so we can rewrite the equation as:

`2^3* 2^y +3=2^3`

Since the bases are equal (base 2), the exponents must also be equal. Therefore, we have:

`3+y+3=3`

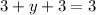
Simplifying gives:

`y+6=3`

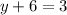
Subtracting 6 from both sides gives:

`y=-3`

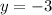
So, the value of y in the equation is -3.

3. The equation is:

`27 * 3^y =3^(2y)`

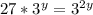
We can rewrite 27 as 3^3, so the equation becomes:

`3^3 *3^y=3^(2y)`

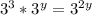
Since the bases are equal (base 3), the exponents must also be equal. Therefore, we have:

`3+y=2y`

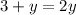
Subtracting y from both sides gives:

`3=y`

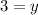
So, the value of y in the equation is 3.