Answer:
The springs from the original pogo stick and the toddler's pogo stick length are equal after 1 second and 0.9994 second.
Step-by-step explanation:
The given functions are:
![\begin{gathered} f(\theta)=2\cos \theta+\sqrt[]{3} \\ g(\theta)=1-\sin ^2\theta+\sqrt[]{3} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/rd7fbp2vp2hlm7o2mndq.png)
The springs from the original pogo stick and the toddler's pogo stick length are equal when both functions coincide
That is;
![\begin{gathered} f(\theta)=g(\theta) \\ \Rightarrow2\cos \theta+\sqrt[]{3}=1-\sin ^2\theta+\sqrt[]{3} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/6v7jff4zeby8icpk4hhm.png)
Solving the equation, we have:
![\begin{gathered} 2\cos \theta+\sqrt[]{3}=1-\sin ^2\theta+\sqrt[]{3} \\ Subtract\sqrt[]{3}\text{ from both sides} \\ 2\cos \theta=1-\sin ^2\theta \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/pzcqd1y0li8rox6uuod7.png)
Note the identity below:
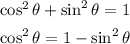
This means
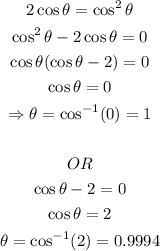
The springs from the original pogo stick and the toddler's pogo stick length are equal after 1 second and 0.9994 second.