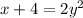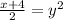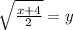Question

What is the inverse of f(x) = 2x2 -4?

Need answers asap

Answer 1

Explanation:

The function doesnt have an inverse. In order for a function to actually have an inverse, it has to pass the horizontal line test. The function above has repeating y-values because of the x^2.

With all this said, you can still find the inverse of the function as long as you restrict the domain (x-values) for the function. So, you cant consider the negative x-values.

First, replace f(x) with y and then switch the x and y variables

`x=2y^2-4`

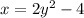
Then solve for y by adding 4 to both sides, dividing by 2, and finally taking the square root.

`x+4=2y^2`

`(x+4)/(2) =y^2`

`\sqrt{(x+4)/(2) }=y`