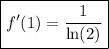Question

Let f(x) = log₂ (x). Find the value of ƒ' (1) .

Answer 1

`f'(1) = (1)/(\ln(2))`

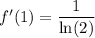
Explanation:

First, we can find the general form of the derivative of a log function using the formula:

`\displaystyle \left[\frac{}{}\log_a(x)\frac{}{}\right]' = (1)/(x\cdot \ln(a))`

For the function at hand:

`f(x) = \log_2(x)`

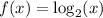
↓ applying the formula

`f'(x) = (1)/(x\cdot \ln(2))`

___

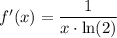
Note: This formula is derived from the log change of base equation:

`\log_a(b) = (\ln(b))/(\ln(a))`

___

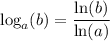
Then, we can plug 1 into the general form of the derivative:

`f'(1) = (1)/(1\cdot \ln(2))`

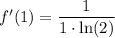
↓ simplifying ... 1/1 = 1

`\boxed{f'(1) = (1)/(\ln(2))}`