Question

In a right triangle, cos (2x) = sin (8x + 5)'. Find the smaller of the triangle's two

acute angles.

Answer 1

According to the given problem,

`\cos (2x)^(\circ)=\sin (8x+5)^(\circ)`

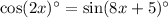
Consider the formula,

`\sin (90-\theta)=\cos \theta`

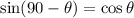
Apply the formula,

`\sin (90-2x)=\sin (8x+5)`

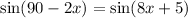
Comparing both sides,

`\begin{gathered} 90-2x=8x+5 \\ 8x+2x=90-5 \\ 10x=85 \\ x=(85)/(10) \\ x=8.5 \end{gathered}`

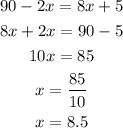
Obtain the value of the two angles,

`\begin{gathered} 2x=2(8.5)=17 \\ 8x+5=8(8.5)+5=73 \end{gathered}`

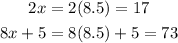
It is evident that the smaller angle is 17 degrees, and the larger angle is 73 degrees.

Thus, the required value of the smaller acute angle of the triangle is 17 degrees.