Question

For the following exercise, rewrite the quadratic functions in standard form and give the vertex. f(x) = x² − 12x + 32

Answer 1

The quadratic function f(x) = x² - 12x + 32 is already in standard form. The vertex of the function is (6, -4).

Step-by-step explanation:

To rewrite the quadratic function in standard form, we need to expand and simplify the expression. In this case, the given function is already in standard form. The standard form of a quadratic function is ax² + bx + c, where a, b, and c are constants. So, the given function is f(x) = x² - 12x + 32.

To find the vertex of the quadratic function, we can use the formula x = -b/2a. In this case, a = 1 and b = -12. So, x = -(-12)/2(1) = 12/2 = 6. Substituting this value in the function, we can find the y-coordinate of the vertex. f(6) = (6)² - 12(6) + 32 = 36 - 72 + 32 = -4. So, the vertex of the given quadratic function is (6, -4).

Answer 2

The quadratic function
`f(x)=x^2-12x+32` can be rewritten in standard form as
`f(x)=(x-6)^2-4,` and the vertex of the parabola is (6, -4).

The standard form of a quadratic function is given by
`f(x) = ax^2 + bx + c,`

where a, b, and c are constants. To rewrite the quadratic function
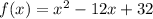`f(x) = x^2 - 12x + 32` in standard form, we'll complete the square.

`f(x) = x^2 - 12x + 32`

`f(x) = (x^2 - 12x) + 32`

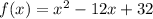
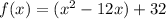
Now, to complete the square, we need to add and subtract
`(b/2)^2` inside the parentheses. In this case, b = -12

`f(x) = (x^2 - 12x + 36 - 36) + 32`

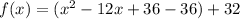
Now, factor the perfect square trinomial and combine like terms:

`f(x) = (x - 6)^2 - 4`

So, the quadratic function
`f(x)=x^2-12x+32` in standard form is
`f(x) = (x - 6)^2 - 4.` Now, the vertex form of a quadratic function is
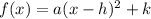`f(x) = a(x - h)^2 + k`, where (h, k) is the vertex of the parabola. Comparing this with the standard form,

we can see that the vertex of
`f(x) = (x - 6)^2 - 4` is (6, -4).