Question

Help with this one please​

Answer 1

a + b + c + d = 0

Explanation:

To determine the sum of a, b, c and d, first find the values of a, b, c and d using the given information.

The given rational function is:

`h(x)=(6x^2+3x)/(2x^2+5x+2)`

`\hrulefill`

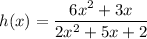
Value of a

Given:

`\displaystyle \lim_{x \to -(1)/(2)}h(x)=a`

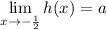
Evaluate h(x) at x = -1/2:

`h\left(-(1)/(2)\right)=(6\left(-(1)/(2)\right)^2+3\left(-(1)/(2)\right))/(2\left(-(1)/(2)\right)^2+5\left(-(1)/(2)\right)+2)=(0)/(0)`

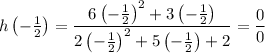
As the limit of h(x) as x approaches -1/2 is an indeterminate form of 0/0, and the numerator and denominator are both differentiable, we can use L'Hôpital's rule to evaluate the limit.

By L'Hôpital's rule:

`\displaystyle \lim_(x \to a)(f(x))/(g(x))&=\lim_(x \to a)(f'(x))/(g'(x))`

Therefore:

`\displaystyle \lim_{x \to -(1)/(2)}(6x^2+3x)/(2x^2+5x+2)&=\lim_{x \to -(1)/(2)} (12x+3)/(4x+5)`

Substitute x = -1/2 into the differentiated numerator and denominator:

`\displaystyle \lim_{x \to -(1)/(2)}(6x^2+3x)/(2x^2+5x+2)&=\lim_{x \to -(1)/(2)} (12x+3)/(4x+5)=(12\left(-(1)/(2)\right)+3)/(4\left(-(1)/(2)\right)+5)=(-3)/(3)=-1`

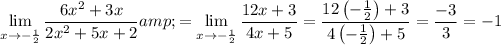
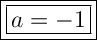
Therefore, the value of a is:

`\Large\boxed{\boxed{a=-1}}`

`\hrulefill`

Value of b

Given h(0) = b, we can find the value of b by substituting x = 0 into the function:

`h(0)=(6(0)^2+3(0))/(2(0)^2+5(0)+2)=(0)/(2)=0`

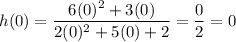
Therefore, since h(0) = 0, then the value of b is:

`\Large\boxed{\boxed{b = 0}}`

`\hrulefill`

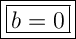
Value of c

The vertical asymptote of a rational function occurs where the denominator equals zero.

Given that the vertical asymptote of h(x) is at x = c, to find the value of c, set the denominator of h(x) equal to zero and solve for x.

First, factor the numerator and denominator:

`h(x)=(3x(2x+1))/((2x+1)(x+2))`

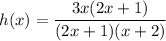
Cancel the common factor (2x + 1):

`h(x)=(3x)/(x+2)`

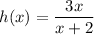
Now, set the denominator equal to zero and solve for x:

`x+2=0 \implies x=-2`

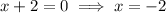
Therefore, since x = c, then the value of c is:

`\Large\boxed{\boxed{c=-2}}`

`\hrulefill`

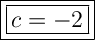
Value of d

We are given that as x approaches infinity, h(x) = d:

`\displaystyle \lim_(x \to \infty)(6x^2+3x)/(2x^2+5x+2)=d`

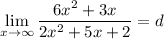
Divide both the numerator and denominator by the highest power of x, which is x²:

`\displaystyle \lim_(x \to \infty)((6x^2)/(x^2)+(3x)/(x^2))/((2x^2)/(x^2)+(5x)/(x^2)+(2)/(x^2))=d`

`\displaystyle \lim_(x \to \infty)(6+(3)/(x))/(2+(5)/(x)+(2)/(x^2))=d`

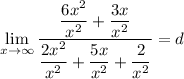
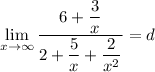
As x approaches infinity, the terms with 1/x and 1/x² become negligible:

`d=(6+0)/(2+0+0)=(6)/(2)=3`

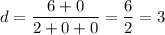
Therefore, the value of d is:

`\Large\boxed{\boxed{d=3}}`

`\hrulefill`

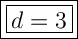
Sum of a, b, c and d

To find the sum of a, b, c and d, simply add together the found values of a, b, c and d:

`\begin{aligned}a+b+c+d&=(-1)+0+(-2)+3\\&=-1+0-2+3\\&=-1-2+3\\&=-3+3\\&=0\end{aligned}`

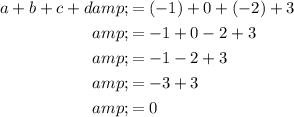
Therefore, the sum of a, b, c and d is zero.

`\Large\boxed{\boxed{a+b+c+d=0}}`