Answer:
See below for proof.
Explanation:
Given trigonometric identity:
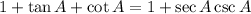
To prove the given trigonometric identity, manipulate the left side to match the right side.
Express tan(A) and cot(A) in terms of sine and cosine using the identities tan(A) = sin(A)/cos(A) and cot(A) = cos(A)/sin(A):
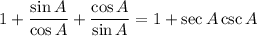
Combine the fractions on the left side of the equation:
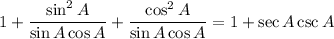

Apply the Pythagorean trigonometric identity, sin²(A) + cos²(A) = 1:

Separate the fractions:
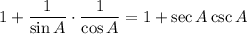
Use the reciprocal trigonometric identities sec(A)=1/cos(A) and cosec(A)=1/sin(A):

Apply the commutative property of multiplication:
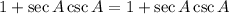
Therefore, the left side is equal to the right side, and the trigonometric identity is proven.