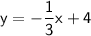Question

Write an equation in slope-intercept form of the line.

Answer 1

Answer:y=-1/3x+4

Explanation:

Slope intercept is the following formula: y=mx+b

In which

m=the slope

b=y-intercept

and y/x are variables

First find the slope (m). You can do this buy using Rise/Run.

Lets find two points, I chose (0,4) and (3,3).

The rise is the change in the y value (4 - 3) and the run is the change in the x value (0 - 3)

4 - 3 = 1 RISE

0 - 3 = -3 RUN

RISE/RUN = SLOPE (m) = -1/3

Your y intercept is 4 because that is where your line crosses the y-axis

So, the answer is y=-1/3x+4

Answer 2

`\sf y = -(1)/(3)x + 4`

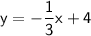
Explanation:

We can find the equation of the line in slope intercept form by taking two points from the line.

Two points are: (0,4) and (3,3)

To find the equation of a line in slope-intercept form y = mx + b, we can use the two points (0,4) and (3,3). The slope (m) can be calculated using these points, and then We can use one of the points to find the y-intercept (b)

First, find the slope (m) using the formula:

`\sf m = (y_2 - y_1)/(x_2 - x_1)`

Using the points (0,4) and (3,3):

`\sf m = (3 - 4)/(3 - 0)`

`\sf m = - (1)/(3)`

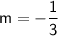
Now that we have the slope, we can use one of the points to find the y-intercept (b).

Let's use the point (0,4):

`\sf 4= (1)/(3)\cdot 0 + b`

Now, solve for b

b = 4

So, the equation of the line in slope-intercept form is:

`\sf y = -(1)/(3)x + 4`