Answer:
7.
x = 30°
(5x)° = 150°
(3x + 60)° = 150°
8.
x = 30°
(3x - 40)° = 50°
(x + 20)° = 50°
Explanation:
Vertically opposite angles are two angles that are formed when two lines intersect. They are opposite each other and share the same vertex. Vertically opposite angles are always equal in measure.
For 7.
In this case:
(5x)° and (3x + 60)° are vertically opposite angles.
So,
(5x)° = (3x + 60)°
5x = 3x + 60
Subtract 3x on both sides.
5x - 3x = 3x + 60 - 3x
2x = 60
Divide both sides by 2.
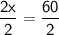
x = 30
We can find the value of each variable by substituting the value of x.
(5x)° = (5×30)° = 150°
(3x + 60)° = (3×30 + 60)° = (90+60)° = 150°
Similarly
For 8.
In this case:
(3x - 40)° and (x + 20)° are vertically opposite angles.
So,
(3x - 40)° = (x + 20)°
3x - 40 = x + 20
Subtract x on both sides.
3x - 40 - x = x + 20 - x
2x - 40 = 20
Add 40 on both sides:
2x - 40 + 40 = 20 + 40
2x = 60
Divide both sides by 2.
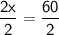
x = 30
We can find the value of each variable by substituting the value of x.
(3x - 40)° = (3×30 - 40)° = (90-40)° = 50°
(x + 20)° = (30 + 20)° = 50°