2 Answers

JRafaelM · Answer 1 · 2024-09-29T08:30:59+0000

SOLUTIONS

How many solutions are there to the equation:

To find the number of solutions to the equation, we need to solve it first.

The given equation is:

$\large\begin{aligned}\rm:\implies 7x - 2(x - 10) = 40\end{aligned}$

Expanding the equation:

$\large\begin{aligned}\rm:\implies 7x - 2x + 20 = 40\end{aligned}$

Combining like terms:

$\large\begin{aligned}\rm:\implies 5x + 20 = 40\end{aligned}$

Subtracting 20 from both sides:

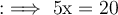
$\large\begin{aligned}\rm:\implies 5x = 20\end{aligned}$

Dividing both sides by 5:

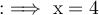
$\large\begin{aligned}\rm:\implies x = 4\end{aligned}$

Hence, the equation has a single solution, which is x = 4.

Nghia Do · Answer 2 · 2024-10-02T17:30:46+0000

One solution

==========

To solve the equation, we can combine like terms and simplify:

Subtract 20 from both sides:

Divide both sides by 5:

So, the equation has one solution, x = 4.