Question

A line passes through the point (-5, -2) and has a slope of 4.

Write an equation in point-slope form for this line.

Answer 1

y = 4x + 18

Explanation:

y + 2 = 4(x + 5)

y + 2 = 4x + 20

y = 4x + 18

Answer 2

SLOPE

A line passes through the point (-5, -2) and has a slope of 4. Write an equation in point-slope form for this line.

Explanation:

The point-slope form of the equation of a line is:

`\large\quad\begin{aligned}\rm\implies \boxed{\rm y - y_1 = m(x - x_1)}\end{aligned}`

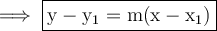
where:

• m is the slope of the line.
• 
  `\sf (x_1, y_1)` is a point on the line.

As per the provided information in the given question, the point on the line is (-5, -2) and the slope of the line is 4.

Substitute the given values into the point-slope form:

`\large\:\:\begin{aligned}\rm:\implies y - (-2) = 4(x - (-5))\end{aligned}`

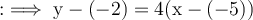
Simplifying this equation, we get:

`\large\qquad\begin{aligned}\rm:\implies y + 2 = 4(x + 5)\end{aligned}`

Hence, the equation of the line in point-slope form is:

`\large\quad\Rrightarrow\:\begin{aligned}\boxed{\boxed{\rm \:\: y + 2 = 4(x + 5)\:\:}}\quad\bigstar\end{aligned}`