Question

Kayden and Josh are practicing a batting cage Josh has hit nine more balls than 1/2 the number of balls that Kayden as if the sum of their heads is 123 how many wars has Josh hit

Answer 1

47

Explanation:

x/2 + 9 + x = 123

2x + 18 + x = 246

3x = 228

x = 76

76/2 = 38 + 9 = 47

Answer 2

BALLS HITTED

Kayden and Josh are practicing a batting cage. Josh has hit nine more balls than 1/2 the number of balls that Kayden as if the sum of their heads is 123, how many balls has Josh hit?

Explanation:

Let's denote the number of balls that Kayden has hit as K.

According to the given information, Josh has hit nine more balls than half the number of balls that Kayden has hit. This can be written as:

`\large\begin{aligned}\qquad\qquad\rm:\implies J = (K)/(2) + 9\end{aligned}`

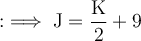
The sum of their hits is given as 123, so we can write the equation:

`\large\begin{aligned}\qquad\qquad\rm:\implies K + J = 123\end{aligned}`

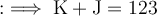
Substituting the value of J from the first equation into the second equation:

`\large\begin{aligned}\rm:\implies K + \left((K)/(2) + 9\right) = 123\end{aligned}`

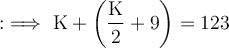
Multiplying through by 2 to eliminate the fraction:

`\large\begin{aligned}\rm:\implies 2K + K + 18 = 246\end{aligned}`

Combining like terms:

`\large\begin{aligned}\rm\qquad:\implies 3K + 18 = 246\end{aligned}`

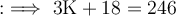
Subtracting 18 from both sides:

`\large\begin{aligned}\qquad\qquad\rm:\implies 3K = 228\end{aligned}`

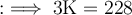
Dividing both sides by 3:

`\large\begin{aligned}\qquad\qquad\rm:\implies K = 76\end{aligned}`

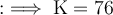
Now, substituting the value of K into the first equation to find J:

`\large\begin{aligned}\qquad\rm:\implies J = (76)/(2) + 9\end{aligned}`

`\large \begin{aligned}\qquad\rm:\implies J = 38 + 9\end{aligned}`

`\large\begin{aligned}\qquad\rm:\implies J = 47\end{aligned}`

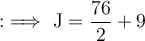
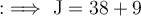
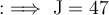
Hence, Josh has hit 47 balls.