Question

Write an equation for the parabola that passes through (1, 12) and has vertex (10, -4)

Answer 1

Answer:
`f(x)=(16)/(81) (x-10)^(2) -4`

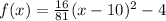
Explanation:

The vertex form of a function defined as
`f(x)=a(x-h)^(2) +k`, where
`(h,k)` is the vertex, and the a-value (
`a`) represents if the graph compresses, stretches, or neither.

The vertex of the parabola is (10,-4), and you can substitute it into the vertex form:
`f(x)=a(x-10)^(2) -4`.

To solve for
`a`, you can input the x- and y-values of a point located on the parabola into the function. We are given the point (1,12) on the graph.

`12=a(1- 10)^(2) -4`

`12=a(-9)^(2) -4`

`12=81a-4`

`16=81a`

`a=(16)/(81)`

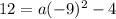
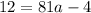
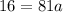
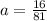
Therefore, the vertex form of the parabola is
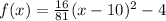`f(x)=(16)/(81) (x-10)^(2) -4`.