Question

In(2x - 1) = 5????????????????

Answer 1

Answer and Step-by-step explanation:

We are trying to solve for x in the equation
`ln(2x - 1) = 5`.

First, we need to get rid of the natural log on the left side. We do this by taking the inverse natural log on both sides.

Follow this formula:
`log_b(M)=N == > M = b^N\\Log Function == > Exponential Function`

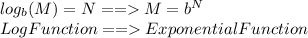
In our case,
`log_b(M)` is
`ln(2x-1)` and
`N` is
`5`.

Note that the Natural Log has a base of e, a mathematical constant known as Euler's number and is approximately 2.71828.

`e^(ln(2x - 1)) = e^(5)\\\\2x - 1 = e^(5)`

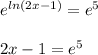
Now, add 1 to both sides of the equation.

`1+ 2x - 1 = e^(5) + 1\\\\2x = e^5+1`

Finally, divide both sides of the equation by 2.

`(2x)/(2) = (e^5+1)/(2) \\\\x = (e^5+1)/(2)`

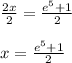
So, the answer is
`x = (e^5+1)/(2)`.