Question

What is an equation of the line that passes through the point (3,-3) and is

parallel to the line 2x + 3y = 15?

Answer 1

Answer: (-2/3)x - 1.

Explanation:

To find an equation of a line that is parallel to the line 2x + 3y = 15 and passes through the point (3, -3), we need to determine the slope of the given line first.

The equation 2x + 3y = 15 is in standard form, where the coefficients of x and y represent the slope of the line. To find the slope, we need to rewrite the equation in slope-intercept form, y = mx + b, where m is the slope.

Let's rearrange the equation 2x + 3y = 15 to solve for y:

3y = -2x + 15

y = (-2/3)x + 5

From the equation y = (-2/3)x + 5, we can see that the slope of the line is -2/3.

Since the line we're looking for is parallel to this line, it will have the same slope of -2/3.

Now that we know the slope (-2/3) and have a point (3, -3) that the line passes through, we can use the point-slope form of a linear equation, y - y1 = m(x - x1), where (x1, y1) is the given point and m is the slope.

Let's substitute the values into the equation:

y - (-3) = (-2/3)(x - 3)

y + 3 = (-2/3)(x - 3)

Now, we can simplify the equation and rewrite it in the slope-intercept form:

y + 3 = (-2/3)x + 2

y = (-2/3)x - 1

Therefore, an equation of the line that passes through the point (3, -3) and is parallel to the line 2x + 3y = 15 is y = (-2/3)x - 1.

Answer 2

`\sf y = -(2)/(3)x - 1`

Explanation:

In order to find the slope of the line 2x + 3y = 15, we can rewrite the equation in slope-intercept form, which is y = mx + b.

To do this, we can subtract 2x from both sides of the equation to get:

2x + 3y- 2x = 15 - 2x

3y = -2x + 15

Dividing both sides of the equation by 3, we get:

`\sf (3y)/(3) = -(2)/(3)x + (15)/(3)`

`\sf y = -(2)/(3)x + 5`

Comparing with slope intercept form, we get

`\sf m = -(2)/(3)x`

Therefore, the slope of the line 2x + 3y = 15 is:

`\sf m = -(2)/(3)x`

Since the parallel lines have same slope, So, slope of another parallel line is also:

`\sf m = -(2)/(3)x`

To find the equation of the line that passes through the point (3,-3) with the same slope as the line 2x + 3y = 15, we can use the point-slope form of linear equations, which is:

`\sf y - y_1 = m(x - x_1)`

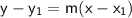
where m is the slope of the line and
`\sf (x_1, y_1)`is a point on the line.

In this case, we know that
`\sf m = -(2)/(3)` and
`\sf (x_1, y_1) = (3,-3)`.

Substituting these values into the equation, we get:

`\sf y - (-3) = -(2)/(3)(x - 3)`

`\sf y + 3 = -(2)/(3)x + 2`

Subtracting 3 from both sides of the equation, we get:

`\sf y + 3 -3= -(2)/(3)x + 2 - 3`

`\sf y = -(2)/(3)x - 1`

Therefore, the equation of the line that passes through the point (3,-3) and is parallel to the line 2x + 3y = 15 in slope intercept form is:

`\sf y = -(2)/(3)x - 1`