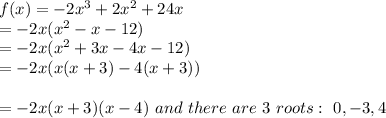Answer:
Hi
Explanation:
The Fundamental Theorem of Algebra states that a polynomial function of degree n has exactly n complex roots (counting multiplicities).
To determine the number of roots for the function
f(x) = -2x^3 + 2x^2 + 24x, we need to find the degree of the polynomial.
The degree of a polynomial is the highest power of the variable in the polynomial expression.
In this case, the highest power of x is 3, so the degree of the polynomial is 3.
According to the Fundamental Theorem of Algebra, this means that the polynomial has exactly 3 complex roots.
Please note that complex roots can be either real or imaginary. Real roots are values of x that make the polynomial equal to zero, while imaginary roots involve the imaginary unit i.
In summary, the function f(x) = -2x^3 + 2x^2 + 24x has exactly 3 complex roots, which can be a combination of real and/or imaginary numbers.