Question

What are the domain and range or this exponentiAl function y=1/6.8×

Answer 1

We want to identify the domain and range of the following function

`(1)/(6)\cdot8^x`

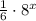
Recall that the domain of a function is the set of values for the variable x, for which the function is defined. Note that we can see this function as the product of two different functions

`(1)/(6)`

and

`8^x`

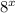
Note that the first part (1/6) does not depend on x, so this means that it is always defined. Also, note that 8^x is always defined for any value of x. That is, if you replace x by any number, you will get another number.

So, this means that the the original function is defined for every value of x. So the domain of this function is the set of all real numbers.

If we define the equation

`y=(1)/(6)\cdot8^x`

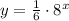
the range is the set of all possible values that y can take. Taking a look at the functions we already identified (1/6, and 8^x) we can see that 1/6 is always a positive number, and we can also see that for every value of x, the number

8^x is always positive.

That means that the product

`(1)/(6)\cdot8^x`

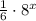
is always a positive number. So, this means that the range of the function is all positive real numbers. That is the set of y such that y>0