Question

Find the value of y.

Find m < AEB

Find m < AEC

Pls show steps, I'm helping my brother with his Geometry hw and I'm also bad at math.

Answer 1

Check the picture below.

`5y-15=3y+5\implies 2y-15=5\implies 2y=20\implies y=\cfrac{20}{2}\implies \boxed{y=10} \\\\\\ (5y-15)+\theta =180\implies 5y-15+\theta =180\implies \stackrel{substituting}{5(10)-15}+\theta =180 \\\\\\ 50-15+\theta =180\implies 35+\theta =180\implies \boxed{\theta =145^o=\measuredangle AEB} \\\\\\ \boxed{\measuredangle AEC}\implies 5y-15\implies \stackrel{substituting}{5(10)-15}\implies 50-15\implies \boxed{35^o}`

Answer 2

m ∠AEB = 145°

m ∠AEC = 35°

Explanation:

Vertically opposite angles are angles that are opposite one another at a specific vertex and are created by two straight intersecting lines. Vertically opposite angles are always equal to each other.

So,

m ∠BED = m ∠AEC

Substitute the given value:

(5y - 15)° = (3y + 5)°

Subtract 3y on both sides.

5y - 15 - 3y = 3y + 5 - 3y

2y - 15 = 5

Add 15 on both sides

2y - 15 + 15 = 5 + 15

2y = 20

Divide both sides by 2.

`(2y)/(2) = (20)/(2)`

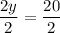
x = 10

Therefore,

m ∠AEC = (5 × 10 - 15)° = ( 50 - 15)° = 35°

Since m ∠AEC and m ∠AEB are pair angles of linear pair. They are supplementary. So,

∠AEC + m ∠AEB = 180°

Substitute the given value:

35° + m ∠AEB = 180°

Subtract 35° on both sides.

35° + m ∠AEB - 35° = 180° - 35°

m ∠AEB = 145°

Therefore,

m ∠AEB = 145°

m ∠AEC = 35°