Question

Gabriella is working two summer jobs, making $16 per hour lifeguarding and making $6 per hour walking dogs. In a given week, she can work no more than 13 total hours and must earn a minimum of $120. If xx represents the number of hours lifeguarding and yy represents the number of hours walking dogs, write and solve a system of inequalities graphically and determine one possible solution.

Answer 1

Explanation: x = number of hours lifeguarding; y = number of hours walking dogs.

Since she can work no more than 13 hours, we will write:
`x+y\leq 13`. Also, since she makes $16 per hour lifeguarding (x) and $6 per hour walking dogs (y), and must earn a minimum of $120, we will write:
`16x+6y\geq 120`.

Hence, we have our system written down. To plot the graph, you will need to isolate y in both equations, thus getting:
`y \leq -x+13` and

`6y\geq -16x+120\\ y\geq (-16x+120)/(6)\\ y\geq (-8x)/(3)+20`

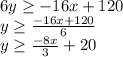
When we plot the graph we get the one in the file attached. So, one possible solution is working 10 hours lifeguarding and 2 hours walking dogs.