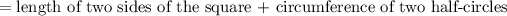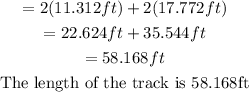Question

I need help with number 5. Here is the problem:Injured runners train on a special track at a rehabilitation center. The track is a square with a half circle on its left and right sides. The area of the square is 128 square feet. What is the length of the track? Use the table to help you answer the questions.

Answer 1

To have a pictorial representation of this problem (the track), we will have the figure below:

To find the length of the track, we will sum up the length of two sides of the square and the circumference of the two half semicircles.

We will find the length of the square thus:

`\begin{gathered} A=l^2 \\ 128=l^2 \\ \sqrt[]{128}=l \\ 11.314ft=l \\ \text{Each side of the square is 11.314ft} \end{gathered}`

Now we will find the circumference of a half-circle:

`=(\pi D)/(2)`

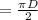
Since the length of the square is also the diameter of the half circle:

`\begin{gathered} D=l=11.314 \\ \text{Circumference of half-circle:} \\ =(\pi(11.314))/(2) \\ =17.772ft \end{gathered}`

The length of the track will be calculated with this expression:

`=\text{length of two sides of the square + circumference of two half-circles}`
`\begin{gathered} =2(11.312ft)+2(17.772ft) \\ =22.624ft+35.544ft \\ =58.168ft \\ \text{The length of the track is 58.168ft} \end{gathered}`