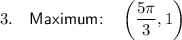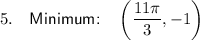Question

Urgent, Trigonometry 100 pts

#4 only, couldn't crop small enough

4. Given the function f(x) = sin(x − 3). Provide (i) the period 7 and (ii) the five key points in the one period that - T includes x = 0.​

Answer 1

(i) T = 4π

(ii) (-π/3, -1), (2π/3, 0), (5π/3, 1), (8π/3, 0), (11π/3, -1)

Explanation:

Given sine function:

`f(x) = \sin\left((1)/(2)x - (\pi)/(3)\right)`

`\hrulefill`

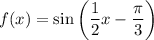
Part (i)

The period of a sine function is the shortest horizontal distance required for the function to complete one full cycle.

The equation to find the period T of a sine function is:

`\boxed{T = (2\pi)/(b)}`

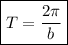
where:

• T is the period of the function.
• b is the coefficient of x inside the sine function.

For the given sine function, the coefficient of x is 1/2. Therefore, the period is:

`T = (2\pi)/((1)/(2)) = 4\pi`

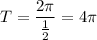
So, the period T is 4π.

`\hrulefill`

Part (ii)

In the context of the sine function, the five key points refer to specific values that help visualize the function's behavior within one period. These points are usually:

• The maximum value (peak).
• The minimum value (trough).
• x-intercepts.

The five key points within one period provide essential information for drawing the graph of the function. By plotting these key points and connecting them to create a smooth waveform, we can sketch the graph accurately. Knowing the period of a function allows the graph to be extended beyond one period by adding the period to the x-value of each key point. This is because the function's behavior repeats itself identically over each period.

For the given function, the 5 key points within the period T = 4π will be:

• Minimum
• x-intercept
• Maximum
• x-intercept
• Minimum

The parent sine function oscillates between y = -1 and y = 1. Since the amplitude of the given function is one, and it has not undergone a vertical shift, the minimum value occurs at y = -1 and the maximum value occurs at y = 1.

To find the x-values of the minimum and maximum points, substitute the corresponding y-values into the function and solve for x.

Minimum points

`\begin{aligned} \sin\left((1)/(2)x - (\pi)/(3)\right)&=-1\\\\(1)/(2)x - (\pi)/(3)&=-(\pi)/(2)\\\\(1)/(2)x&=-(\pi)/(6)\\\\x&=-(\pi)/(3)\end{aligned}`

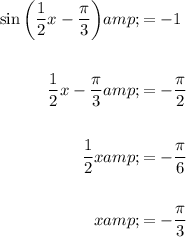
As the period of the function is 4π, the minimum points occur at x = -π/3 + 4πn (where n is an integer). So, the next minimum point after x = -π/3 is:

`x=-(\pi)/(3)+4\pi=(11\pi)/(3)`

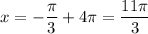
Maximum points

`\begin{aligned} \sin\left((1)/(2)x - (\pi)/(3)\right)&=1\\\\(1)/(2)x - (\pi)/(3)&=(\pi)/(2)\\\\(1)/(2)x&=(5\pi)/(6)\\\\x&=(5\pi)/(3)\end{aligned}`

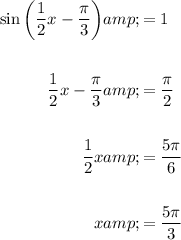
As the period of the function is 4π, the maximum points occur at x = 5π/3 + 4πn (where n is an integer).

x-intercepts

Now, find the x-intercepts by setting the function to zero and solving for x:

`\begin{aligned} \sin\left((1)/(2)x - (\pi)/(3)\right)&=0\\\\(1)/(2)x - (\pi)/(3)&=0,\pi\\\\(1)/(2)x&=(\pi)/(3),(4\pi)/(3)\\\\x&=(2\pi)/(3),(8\pi)/(3)\end{aligned}`

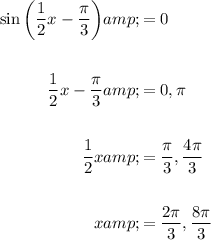
As the period of the function is 4π, the x-intercepts points occur at x = 2π/3 + 4πn and x = 8π/3 + 4πn (where n is an integer).

Five key points

So, the five key points in one period are as follows:

`1.\quad \textsf{Minimum:} \quad \left(-(\pi)/(3),-1\right)`

`2.\quad \textsf{$x$-intercept:} \quad \left((2\pi)/(3),0\right)`

`3.\quad \textsf{Maximum:} \quad \left((5\pi)/(3),1\right)`

`4.\quad \textsf{$x$-intercept:} \quad \left((8\pi)/(3),0\right)`

`5.\quad \textsf{Minimum:} \quad \left((11\pi)/(3),-1\right)`