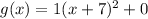Question

Find g(x), where g(x) is the translation 7 units right of f(x)=x2. Write your answer in the form a(x–h)2+k, where a, h, and k are integers.

Answer 1

`g(x) =1(x + 7)^2 + 0`

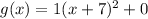
Explanation:

Given

`f(x) = x^2`

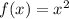
Required

Determine g(x) where g(x) is a translation of f(x), 7 units to the right

When a point is translated to the right, the resulting point is:

`x -> x + b`

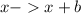
Where b is the number of units to the right.

In this case:

`b = 7`

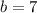
So, we have:

`g(x) = f(x +7)`

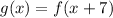
Solving f(x+7)

Substitute x + 7 for x in
`f(x) = x^2`

`f(x + 7) = (x+7)^2`

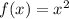
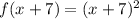
So, we have:

`g(x) = (x+7)^2`

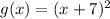
To write in the form of
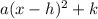`a(x - h)^2 + k`, we have:

`g(x) =1(x + 7)^2 + 0`