Question

Consider the following three point charges: A +3 µC charge at the origin, a +3 µC charge at (3,0,0) cm,

and a-1 uC charge at (0, 6, 0) cm. A uC is 10° coulombs.

(a) Draw a sketch showing the location of the three charges and show the forces acting on the -1 µC charge
due to the other two charges.

(b) Find the net force acting on the -1 µC charge. Write the result as a vector in terms of its components.

(c) Write the net force on the -1 µC charge as a magnitude times a unit vector.

Answer 1

(a) Refer to the attached image.

(b) F_net = <2.68, -12.85> N

(c) ||F_net|| = 13.1 N and F^hat = <0.2, -1.0 >

Step-by-step explanation:

Given three point charges located at distinct points in a three-dimensional space, we are tasked with visually representing their locations and the forces they exert, then computing the net force acting on the -1 µC charge, and finally expressing this force in terms of magnitude and direction. Our solution will involve using Coulomb's law for electric force between charges, vector addition, and concepts of vector magnitude and direction.

`\hrulefill`

Part (a): Sketching the location of the three charges and forces acting on the -1 µC charge.
`\hrulefill`

For part (a), refer to the attached image.

`\hrulefill`

Part (b): Find the net force acting on the -1 µC charge.
`\hrulefill`

The formula for electric force between two charges is given by Coulomb's law:

`\boxed{\left\begin{array}{ccc}\text{\underline{Coulomb's Law:}}\\\\ \vec F=(k_eq_1q_2)/(r^2) \cdot \hat r \\ \\ \text{Where:} \\ \bullet \ k_e \text{ is Coulomb's constant; } 8.99 * 10^9 \ (Nm^2)/(C^2) \\ \bullet \text{ $q_1$ and $q_2$ are the point charges} \\ \bullet \text{ $r$ is the magnitude distance between the charges} \\ \bullet \text{ $\hat r$ is the unit vector that indicates direction}\\\\ \text{Note: $\hat r$ points towards the charge being calculated on.}\end{array}\right}`

Force due to 'q₂' on 'q₁':

`\Longrightarrow \vec F_(1_2)=(k_eq_1q_2)/(r^2) \cdot \hat r_(1_2)\\\\\\\\\Longrightarrow \vec F_(1_2)=((8.99 * 10^9 \ (Nm^2)/(C^2))(-1 * 10^(-6) \ C)(3 * 10^(-6) \ C))/((6 * 10^(-2) \ m)^2) \cdot \frac{\big < 0, \ 6 * 10^(-2) \big > }{\sqrt{(0 )^2+(6 * 10^(-2) )^2} } \\\\\\\\\Longrightarrow \vec F_(1_2)=-7.49 \ N \cdot \big < 0, \ 1\big > \\\\\\\\\therefore \boxed{\vec F_(1_2)= \big < 0, -7.49\big > \ N}`

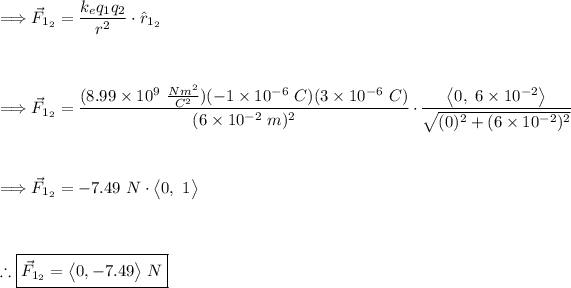
Force due to 'q₃' on 'q₁':

Find 'r' using Pythagorean's theorem.

`\Longrightarrow r=√((6)^2+(3)^2)\\\\\\\\\therefore r=3√(5) \ cm`

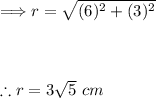
Now finding the force.

`\Longrightarrow \vec F_(1_3)=(k_eq_1q_3)/(r^2) \cdot \hat r_(1_3)\\\\\\\\\Longrightarrow \vec F_(1_3)=((8.99 * 10^9 \ (Nm^2)/(C^2))(-1 * 10^(-6) \ C)(3 * 10^(-6) \ C))/((3√(5) * 10^(-2) \ m)^2) \cdot \frac{\big < -3 * 10^(-2) , \ 6 * 10^(-2) \big > }{\sqrt{(-3 * 10^(-2) )^2+(6 * 10^(-2) )^2} } \\\\\\\\\Longrightarrow \vec F_(1_3)=-5.99 \ N \cdot \big < -0.447, \ 0.894\big > \\\\\\\\\therefore \boxed{\vec F_(1_3)= \big < 2.68, -5.36\big > \ N}`

Using what we have found, we can find the net force acting on charge 'q₁':

`\Longrightarrow \vec F_{\text{net}}=\big < \vec F_{1_(2_x)}+ \vec F_{1_(3_x)}, \ \vec F_{1_(2_y)}+ \vec F_{1_(3_y)}\big > \\\\\\\\\Longrightarrow \vec F_{\text{net}}=\big < 0 + 2.68, \ -7.49+(-5.36)\big > \\\\\\\\\therefore \boxed{\vec F_{\text{net}}=\big < 2.68, \ -12.85\big > \ N}`

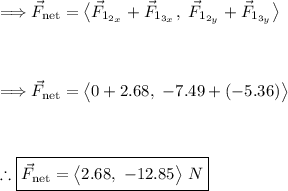
Thus. the net force is found.

`\hrulefill`

Part (c): Write the net force on the -1 µC charge as a magnitude times a unit vector.
`\hrulefill`

The magnitude of the net force can be calculated as follows:

`\Longrightarrow \big|\big| \vec F_{\text{net}} \big|\big|=\sqrt{(\vec F_{\text{net}_x})^2+(\vec F_{\text{net}_y})^2}\\\\\\\\\Longrightarrow \big|\big| \vec F_{\text{net}} \big|\big|=√((2.68)^2+(-12.85)^2)\\\\\\\\\therefore \boxed{\big|\big| \vec F_{\text{net}} \big|\big|=13.1 \ N}`

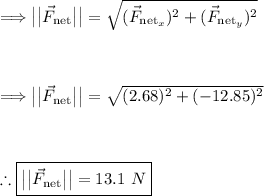
The unit vector can be calculated as follows:

`\Longrightarrow \hat F_{\text{net}} =\frac{\big < \vec F_{\text{net}_x}, \ \vec F_{\text{net}_y} \big > }{\sqrt{(\vec F_{\text{net}_x})^2+(\vec F_{\text{net}_y})^2}} \\\\\\\\\Longrightarrow \hat F_{\text{net}} =(\big < 2.68, \ -12.85 \big > )/(13.1) \\\\\\\\\Longrightarrow \hat F_{\text{net}} =\big < (2.68)/(13.1), \ (-12.85)/(13.1) \big > \\\\\\\\\therefore \boxed{\hat F_{\text{net}} =\big < 0.20, -1.0\big > }`

Thus, the magnitude and the unit vector is found.