Question

Use the diagram below to find the area of the shaded sector

Answer 1

We need to get the slopes of the lines A and B.

Slope of A considering the points (-4, 3) and (0, 0) which is at the origin, we have

`\begin{gathered} m=(0-3)/(0-(-4)) \\ m=(-3)/(4) \\ m=-(3)/(4) \end{gathered}`

Since line B is a horizontal line, the slope is 0.

angle between two slopes is given as

`\begin{gathered} tan\theta=|(m_2-m_1)/(1+m_1m_2)| \\ where\text{ }\theta\text{ is the angle between them and } \\ m_1\text{ and m}_2\text{ are slopes of the line } \end{gathered}`

So, we have

`\begin{gathered} tan\theta=|(m_2-m_1)/(1+m_1m_2)| \\ tan\theta=|(0-(-(3)/(4)))/(1+0(-(3)/(4)))| \\ tan\theta=|((3)/(4))/(1)| \\ tan\theta=|(3)/(4)| \\ tan\theta=(3)/(4) \\ \theta=tan^(-1)(3)/(4) \\ \theta=36.86989 \\ \theta=36.87\degree \end{gathered}`

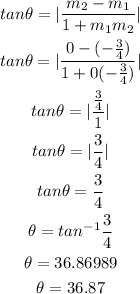
Hence the angle between A and B is 36.87 degrees

Area of a sector is given as

`A=(\theta)/(360\degree)*\pi r^2`

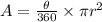
Note that the radius r is the length of line B, which is 5 units. So, the area becomes

`\begin{gathered} A=(\theta)/(360\degree)*\pi r^2 \\ A=(36.87)/(360)*\pi*5^2 \\ A=8.04376\text{ units}^2 \end{gathered}`

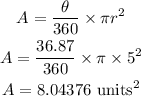
Hence the answer is 8.04 square units. The last option is the answer