Question

I need help to solve. This is my daily practice assignment

Answer 1

The scenario formed a right triangle with an adjacent side of 24.2 ft. and included an angle of 37°.

First, let's recall the three main trigonometric functions.

`\text{ Sine }\Theta\text{ = }\frac{Opposite\text{ Side}}{\text{Hypotenuse}}`
`\text{ Cosine }\Theta\text{ = }\frac{Adjacent\text{ Side}}{Hypotenuse}`
`\text{ Tangent }\Theta\text{ = }\frac{Opposite\text{ Side}}{Adjacent\text{ Side}}`

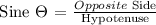
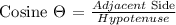
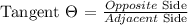
In the scenario, the height of the flagpole appears to be the Opposite Side of the right triangle formed.

Since the function that we will be equating involves the Opposite Side and Adjacent Side of a right triangle, we will be applying the Tangent Function to find the height of the flagpole.

We get,

`\text{ Tangent }\Theta\text{ = }\frac{Opposite\text{ Side}}{Adjacent\text{ Side}}`
`Tangent(37^(\circ))\text{ = }(x)/(24.2)`
`\text{ Tangent (37}^(\circ))\text{ x 24.2 = x}`
`\text{ 18.23600801249 = x}`
`\text{ 18.2 ft. }\approx\text{ x}`

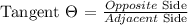
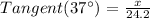
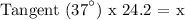
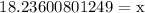
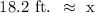
Therefore, the height of the flagpole is 18.2 ft.