Question

PLEASE HELP WILL IGVE BRIANLIEST AND 100 POINTS

Answer 1

The correct answer is option 1: -4 only

For a limit to exist itself, each side of the limit must approach the same point from the left and right of it.

For example at x=-4 each side of that point reaches the same point.

A term to describe points that fit these descriptions is Continuous.

Points such as x=-5 and x=-2 and not continuous due to having a jump between left and right of the point.

From the options provided, only -4 has a continuous point with no jumps.

Answer 2

A) -4 only

Explanation:

A limit is said to exist when a function approaches a specific finite value as the input variable approaches a specific point. This convergence is deemed valid when it is achieved consistently from both the left and right sides of that specified point.

`\boxed{\begin{array}{c}\textsf{If\;$f(x)$\;is\;continuous\;at\;$x=c$\;then:}\\\\\displaystyle \lim_(x \to c^(-))f(x)=f(c)\qquad\lim_(x \to c^(+))f(x)=f(c)\qquad \lim_(x \to c)f(x)=f(c)\end{array}}`

From observation of the given graph, the function f(x) approaches x = -2 consistently from both the left and right sides when x = -4:

`\displaystyle \lim_(x \to -4^-)f(x)=-2\qquad \displaystyle \lim_(x \to -4^+)f(x)=-2\qquad \displaystyle \lim_(x \to -4)f(x)=-2`

Therefore, as:

`\displaystyle \lim_(x \to -4^-)f(x)= \lim_(x \to -4^+)f(x)=\lim_(x \to -4)f(x)=-2`

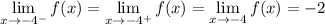
Then, f(x) is continuous at x = -4.

`\hrulefill`

Additional Notes

When x = -2, the left side approaches y = -2, but the right side approaches y = 0. Therefore, f(x) is not continuous at x = -2.

When x = -5, the left side approaches y = -2, but the right side approaches y = -5. Therefore, f(x) is not continuous at x = -5.