Question

Just wondering if any of this is right, if I got something wrong please explain how to properly solve. also need help with #10!!!

Answer 1

m∠G = 45°

Explanation:

#10

Given:

The triangle is right angled isoceles triangle since AN = NG and m∠N = 90°.

To find:

m∠G = ?

Solution:

Since the triangle is a right angled isosceles triangle, we know that the two acute angles are equal.

Therefore, m∠G = m∠A.

We also know that the sum of the angles in a triangle is 180 degrees. Therefore, we can write the following equation:

m∠G + m∠N + m∠A = 180°

Substituting in the known values, we get:

m∠G + 90° + m∠A = 180°

Subtracting 90° from both sides of the equation, we get:

m∠G + m∠A = 180° - 90°

m∠G + m∠A = 90°

Since m∠G = m∠A

m∠G + m∠G = 90°

2m∠G = 90°

Divide both sides of the equation by 2 to find the value of each angle:

`\sf m\angle G = (90^\circ)/(2)`

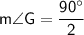
m∠G = 45°

Therefore, m∠G = 45°