Question

in a right triangle the sum of the squares of the two shorter side is equal to the square of the longest side if the longest side of a right angle is 13 inches and the shortest side is 5 inches what is the length of the last side

Answer 1

Answer: 12 inches

Explanation:

In a right triangle, the sum of the squares of the two shorter sides is equal to the square of the longest side. This is known as the Pythagorean theorem. Let's denote the longest side as c, and the two shorter sides as a and b. According to the Pythagorean theorem, we have the equation: a^2 + b^2 = c^2 Given that the longest side (c) is 13 inches and one of the shorter sides (a) is 5 inches, we can substitute these values into the equation: 5^2 + b^2 = 13^2 25 + b^2 = 169 To find the length of the other side (b), we need to isolate it on one side of the equation. Subtracting 25 from both sides, we get: b^2 = 144 To solve for b, we take the square root of both sides: b = √144 b = 12 Therefore, the length of the last side is 12 inches.

Answer 2

12 inches

Explanation:

To find the length of the last side of a right triangle, we can use the Pythagorean Theorem, which states that the square of the hypotenuse (longest side) is equal to the sum of the squares of the other two sides.

In this case, the hypotenuse is 13 inches and one of the shorter sides is 5 inches. We can use the Pythagorean Theorem to solve for the length of the other shorter side as follows:

`\sf a^2 + b^2 = c^2`

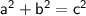
Where:

• a is the length of one of the shorter sides (5 inches)
• b is the length of the other shorter side (unknown)
• c is the length of the hypotenuse (13 inches)

Substituting the known values into the equation, we get:

`\sf 5^2 + b^2 = 13^2`

`\sf 25 + b^2 = 169`

Subtracting 25 from both sides of the equation, we get:

`\sf b^2 = 169 - 25`

`\sf b^2 = 144`

Taking the square root of both sides of the equation, we get:

`\sf b = √(144)`

b = 12

Therefore, the length of the other shorter side is 12 inches.