Question

At x = 2, the function the piecewise function 2 times x plus 2 for x is less than or equal to 2 and 2 times x to the second power minus 2 for x is greater than 2 is considered which of the following?

Answer 1

Step-by-step explanation:

A, Do it was the first time what

Answer 2

The correct answer is option A. Both continuous and differentiable.

To determine the continuity and differentiability of the given piecewise function
`\( f(x) \)`, we need to check the conditions at the point
`\( x = 2 \)` where the function changes its definition.

For continuity:

A function is continuous at a point
`\( x = a \)` if the following three conditions are met:

1.
`\( f(a) \)` is defined.

2. The limit of
`\( f(x) \)` as
`\( x \)` approaches
`\( a \)` from the left
`(\( \lim_{{x \to a^-}} f(x) \))` exists.

3. The limit of
`\( f(x) \)` as
`\( x \)` approaches
`\( a \)` from the right
`(\( \lim_{{x \to a^+}} f(x) \))` exists.

4.
`\( \lim_{{x \to a^-}} f(x) = \lim_{{x \to a^+}} f(x) = f(a) \)`

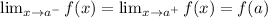
For differentiability:

A function is differentiable at a point
`\( x = a \)` if the following condition is met:

1. The derivative
`\( f'(a) \)` exists.

Now let's analyze the given function at \( x = 2 \):

1. For continuity:

-
`\( f(2) = 2(2) + 2 = 6 \)`

-
`\( \lim_{{x \to 2^-}} f(x) = \lim_{{x \to 2^-}} (2x + 2) = 6 \)`

-
`\( \lim_{{x \to 2^+}} f(x) = \lim_{{x \to 2^+}} (2x^2 - 2) = 6 \)`

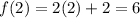
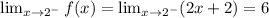
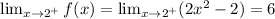
- The above limits and
`\( f(2) \)` are equal, so the function is continuous at
`\( x = 2 \).`

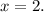
2. For differentiability:

- The derivative
`\( f'(x) \)` exists for both
`\( 2x + 2 \)` and
`\( 2x^2 - 2 \)` at
`\( x = 2 \)`, so the function is differentiable at
`\( x = 2 \)`.

Therefore, the correct answer is A. Both continuous and differentiable.