Question

If the area of a sector is 100 ft^2 and the radius of the circle is 22 ft what is the central angle measure for that sector and what is the length of the arc

Answer 1

`\displaystyle \theta=0.413\ rad`

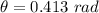
L= 9.086 feet

Explanation:

Area of a Circular Sector

Given a circle of radius r, the area of a circular sector defined by a central angle θ (in radians) is given by

`\displaystyle A=(1)/(2)r^2\theta`

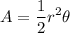
And the length of the arc is:

`L=\theta r`

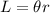
We know the area of the sector is 100 square feet and the radius is r=33 ft, thus:

`\displaystyle 100=(1)/(2)r^2\theta`

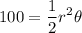
Solving for θ:

`\displaystyle \theta=(200)/(r^2)`

`\displaystyle \theta=(200)/(22^2)`

`\displaystyle \theta=0.413\ rad`

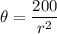
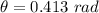
The arc length is:

`L=0.413* 22`

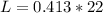
L= 9.086 feet