Answer:

Explanation:
We are given that:
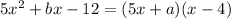
First, we can distribute the right-hand side:

Distribute:
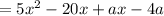
Rewrite:
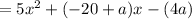
Since it is equivalent to the above expression, the coefficients of the variables must match. This means that:
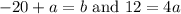
Solving for a in the second equation gives:
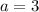
Therefore:
