The concentration of iron in the sample in parts per million is
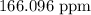
How to determine the concentration of iron in the sample in parts?
Given data:
Volume of sample = 100 mL
Volume of
 = 25 mL
= 25 mL
Molarity of
 = 0.002517 M
= 0.002517 M
Volume of
 solution = 8.53 mL
solution = 8.53 mL
Molarity of
 solution = 0.00949 M
solution = 0.00949 M
Equation used:
Concentration in ppm =
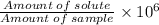
Solution:
Six equivalents of
 react with one equivalent of
react with one equivalent of
 .
.
Milliequivalents of
 taken =
taken =
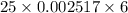
Milliequivalents of excess
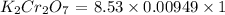
Milliequivalents of
 in water =
in water =

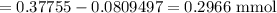
Mass of
 in water sample =
in water sample =

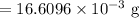
Concentration in parts per million:
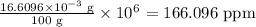
Therefore, the concentration of iron in the sample in parts per million is
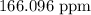 .
.
Complete question:
A 100.0-mL sample of spring water was treated to convert any iron present to Fe21. Addition of 25.00-mL of 0.002517 M K2Cr2O7 resulted in the reaction 6Fe2+ + Cr2O7 2- + 14H+ → 6Fe3+ + 2Cr3+ + 7H2O
The excess K2Cr2O7 was back-titrated with 8.53 mL of 0.00949 M Fe2+ solution. Calculate the concentration of iron in the sample in parts per million.