Question

What is the equation of a sine function with an amplitude of 2 and a period of 4π? A) y = 2sin(2x) B) y = sin(4x) C) y = 2sin(x) D) y = 2sin(4x)

Answer 1

The equation of a sine function with an amplitude of 2 and a period of 4π is represented as
`\( y = 2 \sin(4x) \)`. (option D)

Why is this correct?

The equation of a sine function with an amplitude
`(\(A\))` and a period (\
`(P\))` is given by:

`\[ y = A \sin\left((2\pi)/(P)x\right) \]`

Given:

Amplitude
`(\(A\)) = 2`

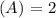
Period
`(\(P\)) = \(4\pi\)`

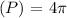
Substituting these values into the equation:

`\[ y = 2 \sin\left((2\pi)/(4\pi)x\right) \]`

`\[ y = 2 \sin\left((1)/(2)x\right) \]`

Comparing this equation with the provided options:

A)
`\(y = 2\sin(2x)\)` - This has an amplitude of 2 but a different period not
`\ 4\pi\)` ).

B)
`\(y = \sin(4x)\)` - This has a different amplitude and a period of
`\((\pi)/(2)\)`, not
`\(4\pi\)`.

C)
`\(y = 2\sin(x)\)` - This has the correct amplitude of 2 but a period of
`\(2\pi\)`, not
`\(4\pi\)`.

D)
`\(y = 2\sin(4x)\)` - This has both the correct amplitude of 2 and the correct period of
`\(4\pi\)`.

Therefore, the correct answer is: D)
`\(y = 2\sin(4x)\)`