Question

Anand knows from experience that if he does not review a new vocabulary word that he has learned, that he has a 70% percent chance of forgetting it each day. Let D be the number of days Anand goes without reviewing a word until he forgets it.

Answer 1

Anand is likely to forget the word after 1 day without review.

To solve this problem, we'll model the likelihood of Anand remembering a vocabulary word over multiple days without review. We know that each day, Anand has a 70% chance of forgetting a word he does not review. Let's denote the probability of Anand remembering a word after D days as P(D) .

Here's the step-by-step breakdown:

Step 1: Define the Probability of Forgetting Each Day

The probability of forgetting a word on any given day is 70%, or 0.7. Therefore, the probability of remembering the word on any given day is 1 - 0.7 = 0.3 (since the probabilities of all possible outcomes must sum up to 1).

Step 2: Express the Probability of Remembering After Multiple Days

The probability of remembering the word after D days without review, P(D) , is the product of the probability of remembering the word each day, raised to the power of D days:

`\[ P(D) = 0.3^D \]`

Step 3: Determine the Day on Which Anand Forgets the Word

Anand forgets the word when the probability of remembering falls below a certain threshold (which can be considered as when it becomes more likely for him to forget than to remember). In this case, we need to find the first day D when P(D) is less than 0.5 (50%), since at this point, it's more likely that he will forget the word than remember it.

We are looking for the smallest integer D such that P(D) < 0.5 . We solve for D in the inequality:

`\[ 0.3^D < 0.5 \]`

Step 4: Solve the Inequality for D

To solve this inequality, we can take the logarithm of both sides. It's convenient to use the natural logarithm (ln):

`\[ \ln(0.3^D) < \ln(0.5) \]`

`\[ D \cdot \ln(0.3) < \ln(0.5) \]`

Since
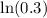`\( \ln(0.3) \)` is negative, when we divide both sides of the inequality by
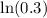`\( \ln(0.3) \)`, the direction of the inequality changes:

`\[ D > (\ln(0.5))/(\ln(0.3)) \]`

Let's calculate this value to determine D .

The calculation gives us
`\( D \approx 0.576 \).` Since D represents whole days, we need to consider the smallest integer greater than this value to find the day on which Anand is more likely to forget the word. In this case, rounding up D to the nearest whole number gives us:

D = 1