Question

A 36-foot flagpole casts a 10-foot shadow,

4
while the hospital nearby casts a 37--foot
8
shadow. Find the height of the hospital.

Answer 1

126 feet

Explanation:

To find the height of the hospital, we can use similar triangles. The flagpole and its shadow form one triangle, and the hospital and its shadow form another, similar triangle.

The ratio of the corresponding sides of similar triangles is the same.

So, we can set up a proportion using the heights and their corresponding shadow lengths:

`\sf \frac{\textsf{Flagpole height }(H_1) }{\textsf{ Flagpole shadow length} (S_1) } =\frac{\textsf{Hospital height} (H_2) }{\textsf{Hospital shadow length} (S_2)}`

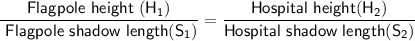
Given:

• Flagpole height (H1) = 36 feet
• Flagpole shadow length (S1) =
  `\sf 10 (3)/(4) =(10\cdot 4 + 3)/(4) = (43)/(4) feet`
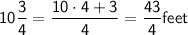
• Hospital shadow length (S2) =
  `\sf 37 (5)/(8) =(37\cdot 8 + 5 )/(8) = (301)/(8) feet`

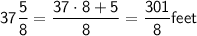
Now, let's find H2 (Hospital height):

`\sf (H_1 )/( S_1) =( H_2 )/( S_2)`

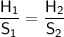
Substitute the given value and simplify for H2.

`\sf (36 )/( (43)/(4)) =( H_2 )/( (301)/(8) )`

`\sf 36 \cdot (4)/(43) =H_2 \cdot (8)/(301)`

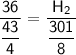
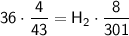
Doing Criss cross Multiplication:

`\sf 36 \cdot (4)/(43) \cdot (301)/(8) =H_2`

`\sf H_2 = ( 36\cdot 4 \cdot 301)/(43 \cdot 8 )`

`\sf H_2 = (43344)/(344)`

`\sf H_2 = 126`

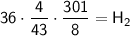
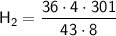
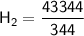
So, the height of the hospital is 126 feet.