Question

A boy throws a ball into the air. The equation h = -16t^2 + 28t + 3 models the path of the ball, where h is the height in feet of the ball r seconds after it is thrown. How long is the ball in the air? Round your answer to the nearest tenth of a second. a) -0.1 seconds b) 3.7 seconds c) 1.9 seconds d) 0.9 seconds

Answer 1

The ball is in the air for approximately 1.9 seconds, obtained by solving the quadratic equation for time when the height is zero.

Step-by-step explanation:

The question asks how long a ball thrown into the air is in the air, based on the quadratic equation
`h = -16t^2 + 28t + 3.`To find this, we need to determine when the ball will hit the ground, which is when h (the height) equals zero. Setting the equation equal to zero and solving for t using the quadratic formula will give us two solutions. Since time cannot be negative, we disregard the negative solution and consider only the positive solution.

Using the quadratic formula to solve -16t2 + 28t + 3 = 0, we find that the ball is in the air for approximately 1.9 seconds when rounded.

Answer 2

Based on the given information, the ball is in the air for approximately 1.9 seconds. Therefore, the answer is c) 1.9 seconds.

How to determine how long the ball is in the air

To determine how long the ball is in the air, find the time at which the height of the ball (h) is equal to zero, as that represents the time when the ball reaches the ground.

The given equation is

`h = -16t^2 + 28t + 3`

where

h is ball height (ft)

t is the time (s)

When we set h = 0

`-16t^2 + 28t + 3 = 0`

To solve this quadratic equation, use the quadratic formula:

t = (-b ± √(
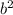`b^2` - 4ac)) / (2a)

In this case, a = -16, b = 28, and c = 3.

Plug in these values into the formula above

t = (-28 ± √(
`28^2` - 4(-16)(3))) / (2(-16))

t = (-28 ± √(784 + 192)) / (-32)

t = (-28 ± √976) / (-32)

t = (-28 ± √976) / (-32)

t₁ = (-28 + √976) / (-32) ≈ 1.9 seconds

t₂ = (-28 - √976) / (-32) ≈ -0.1 seconds

Since time cannot be negative in this context, take the second value of t

Hence, the ball is in the air for approximately 1.9 seconds.

Therefore, the answer is c) 1.9 seconds.