Question

variance and standard deviation The following scores on an exam are given below: 52, 84, 75, 70, 71, 57, 68 a. Compute the mean (round to the nearest tenth). Justify your answer. b. Compute sum of the squares (construct a table) c. Compute the variance. d. Compute the standard deviation (round to the nearest tenth). Justify your answer.​

Answer 1

Part (a)

A spreadsheet is recommended for stats problems like this.

To compute the mean, use the function named "Average". Or you could add up the values using the function named "Sum". Then divide over the sample size 7.

To get the mean in general, we add up the values and divide over the sample size.

The approximate result should be roughly 68.1428571428571, which rounds to 68.1

Answer: Mean = 68.1 approximately

--------------------------------------------------------------------------------

Part (b)

The table would look like this

`\\\mu = \text{mean}\\\\\begin{array}c \cline{1-2}\text{x} & (\text{x}-\mu)^2\\\cline{1-2}52 & 260.5918\\\cline{1-2}84 & 251.449\\\cline{1-2}75 & 47.0204\\\cline{1-2}70 & 3.449\\\cline{1-2}71 & 8.1633\\\cline{1-2}57 & 124.1633\\\cline{1-2}68 & 0.0204\\\cline{1-2}\text{Total} & 694.8572\\\cline{1-2}\end{array}`

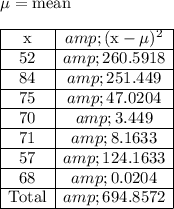
We subtract the mean from each data value. Then square the difference. After that is done, we add up all of the results.

I used the un-rounded version of the mean to get the best accuracy possible.

Answer: Sum of squares is roughly 694.9

--------------------------------------------------------------------------------

Part (c)

SSE = sum of squared error

SSE = 694.8572 found in part (b)

Divide the SSE over n = 7 to get the population variance. Divide over n-1 = 7-1 = 6 to get the sample variance.

I'll use the population version.

694.8572/7 = 99.265314

Answer: Population variance is roughly 99.3

--------------------------------------------------------------------------------

Part (d)

standard deviation = sqrt(variance)

standard deviation = sqrt(99.265314)

standard deviation = 9.9632

standard deviation = 10.0

Answer: Population standard deviation is 10.0 approximately