Question

Algebra ( Need urgent help please! )​

Answer 1

Answer: Great Question! Answer and work Below.

Step-by-step explanation:

Let's first use the information we are given :

`x^a = y^b = z^c` and
`y^3=xz`

We then need to prove that
`3/b = 1/a = 1/c`

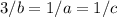
Manipulate the terms to equal one exponential value(I chose x):

`y=x^a/b` and
`z=x^c/b`

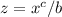
Next, you can substitute the value of y into the second eq to solve a,b,c:

`x^(3a/b)=x * x^(c/b)` (Plug in the y and z val, since y is cubed we multiply the numerator by 3)

Now since all the bases are the same, we can remove the x from the equation :

`3a/b = 1+c/b`

`3a/b = (b+c)/b`

`3a = b+c`

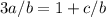
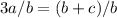
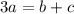
Now Substitute :

`3/b = 3/(3a/c) = c/a = 1/a+1/c`

and we have proved the final equation!

That's it!

Answer 2

See below for proof.

Explanation:

Given equations:

`x^a=y^b=z^c`

`y^3=xz`

To prove that 3/b = 1/a = 1/c, isolate x and z and represent them as expressions with a common base of y.

`\textsf{For $x^a=y^b$, isolate $x$ by taking the $a$-th root of both sides of the equation:}`

`\left(x^a\right)^{(1)/(a)}=\left(y^b\right)^{(1)/(a)}`

Apply the power of a power exponent rule:

`x^{(a)/(a)}=y^{(b)/(a)}`

`x^(1)=y^{(b)/(a)}`

`x=y^{(b)/(a)}`

`\textsf{For $z^c=y^b$, isolate $z$ by taking the $c$-th root of both sides of the equation:}`

`\left(z^c\right)^{(1)/(c)}=\left(y^b\right)^{(1)/(c)}`

Apply the power of a power exponent rule:

`z^{(c)/(c)}=y^{(b)/(c)}`

`z^(1)=y^{(b)/(c)}`

`z=y^{(b)/(c)}`

Now, substitute the expressions for x and z into y³ = xz:

`y^3 =y^{(b)/(a)}\cdot y^{(b)/(c)}`

Combine the terms on the right side using the product exponent rule:

`y^3 =y^{(b)/(a)+(b)/(c)}`

Since the bases are the same (y), the exponents must be equal:

`3 = (b)/(a) + (b)/(c)`

Divide all terms by b:

`(3)/(b) = (b)/(ab) + (b)/(cb)`

Simplify:

`(3)/(b) = (1)/(a) + (1)/(c)`

Hence, we have proven that 3/b = 1/a = 1/c.