Question

Consider the polynomial function: p(x) = 2x³ +5x²-kx+6, where k is an unknown real number. If P(x) is divided by (x-2), the

remainder is 37. What is the value of k?

Answer 1

k =
`(5)/(2)`

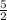
Explanation:

the remainder theorem states that if o polynomial p(x) is divided by the factor (x - a) , then the remainder is p(a)

given

p(x) = 2x³ + 5x² - kx + 6 , divided by (x - 2) , then

p(2) = 37

substitute x = 2 into p(x) , equate to 37 and solve for k

2(2)³ + 5(2)² - 2k + 6 = 37

2(8) + 5(4) - 2k + 6 = 37

16 + 20 - 2k + 6 = 37

42 - 2k = 37 ( subtract 42 from both sides )

- 2k = - 5 ( divide both sides by - 2 )

`(-2)/(-2)` k =
`(-5)/(-2)` , that is

k =
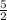`(5)/(2)` = 2.5