Question

One of the roots of the equation ax²+bx+c=0 is twice the other, show that 2b²=9ac

Answer 1

If one root of the equation ax² + bx + c = 0 is twice the other, then 2b² = 9ac.

Explanation:

To show that 2b² = 9ac, if one of the roots of the equation ax² + bx + c = 0 is twice the other, we can Vieta's formulas.

Vieta's formulas are a set of mathematical relationships that express the coefficients of a polynomial equation in terms of its roots.

`\boxed{\begin{array}{l}\underline{\textsf{Vieta's Formula for Quadratic Equation}}\\\\\textsf{If $f(x) = ax^2+ bx + c$ has roots $\alpha$ and $\beta$ then:}\\\\\textsf{Sum of the roots:}\quad \alpha+\beta=-(b)/(a)\\\\\textsf{Product of the roots}\quad \alpha\cdot\beta=(c)/(a)\end{array}}`

Given that one of the roots is twice the other, then the two roots are r and 2r.

Using Vieta's formulas, we have:

`\textsf{Sum of the roots:}\quad r+2r=-(b)/(a)\implies 3r=-(b)/(a)`

`\textsf{Product of the roots}\quad r\cdot 2r=(c)/(a)\implies 2r^2=(c)/(a)`

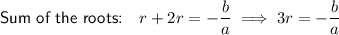
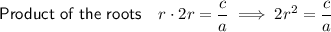
Rearrange the product equation to isolate r²:

`r^2=(c)/(2a)`

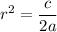
Square the sum equation:

`(3r)^2=\left(-(b)/(a)\right)^2`

`9r^2=(b^2)/(a^2)`

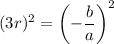
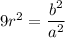
Substitute the expression for r² into the expression for 9r²:

`9\left((c)/(2a)\right)=(b^2)/(a^2)`

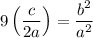
Switch sides:

`(b^2)/(a^2)=9\left((c)/(2a)\right)`

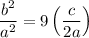
Divide both sides by a:

`(b^2)/(a)=(9c)/(2)`

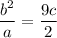
Cross multiply:

`2b^2=9ac`

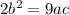
Therefore, we have shown that if one root of the equation ax² + bx + c = 0 is twice the other, then 2b² = 9ac.