Question

A convention manager finds out she has 1480$ made up of twenty fifties. She has a total of 47 bills how many fifty-dollar bills does the manager have?(NEED ANSWER ASAP!)

Answer 1

Answer: 29 twenties and 18 fifties

Explanation:

You can solve this by making a system of equations.

Let x = the number of twenty dollar bills

Let y = the number of fifty dollar bills

x + y = 47 (she has a total of 47 bills)

20x + 50y = 1480 (she has $1480)

If you solve the first equation for x you can use substitution.

x = 47 - y

20(47 - y) + 50y = 1480

940 -20y + 50y = 1480

30y = 540

y = 18

Then you plug the 18 into one of the equations

x + 18 = 47

x = 29

Answer 2

18 fifty-dollar bills

Explanation:

To solve this problem, we can use a system of two equations.

Let x be the number of twenty-dollar bills and y be the number of fifty-dollar bills.

We know that the total number of bills is 47 and the total amount of money is $1480.

x + y = 47

20x + 50y = 1480

We can solve this system of equations using elimination. Multiplying the first equation by -20, we get:

-20x - 20y = -940

Adding this equation to the second equation, we get:

20x + 50y + (-20x - 20y) = 1480 + (-940)

20x + 50y - 20x - 20y = 1480 - 940

30y = 540

Dividing both sides by 30, we get:

`\sf (30y )/(30)=( 540)/(30)`

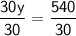
y = 18

Therefore, the manager has 18 fifty-dollar bills.