Question

From base camp, a park ranger drives 27 meters at 32 degrees East of North, then 40 meters at 58 degrees West of North, and finally 39 meters directly West in an attempt to rescue a lost hiker.

Answer 1

R = 73.34 m, θ = 37º North of West

Step-by-step explanation:

In this exercise you are asked to find the distance traveled.

The best way to do this is with a Cartesian coordinate system, let's use a system where the x axis coincides with the West - East direction), to decompose the trajectories

First trajectory

distance d₁ = 27 m

Direction 32 East of North, this angle is measured from the vertical direction (y-axis)

cos 32 = y₁ / d₁

sin 32 = x₁ / d₁

y₁ = d₁ cos 32

x₁ = d₁ sin 32

y₁ = 27 cos 32 = 22.90 m

x₁ = 27 sin 32 = 14.31 m

second trajectories

distance d2 = 40 m

direction 58 West from North, the angle is measured with respect to the y axis, towards the negative side of the x axis

cos 58 = y₂ / d₂

sin 32 = x₂ / d₂

y₂ = d₂ cos58

x₂ = d₂ sin 58

y₂ = 40 cos 58 = 21.20 m

x₂ = 40 sin 58 = -33.92 m

The negative sign of the x coordinate is due to the fact that the displacement is towards the West (negative of the x axis)

third trajectory

distance d₃ = 39 m

West direction, negative part of x-axis

x₃ = - 39 m

the total distance is

= x₁ + x₂ + x₃

X_{total}l = 14.30 - 33.92 -39

X_{total}X_total = -58.6 m

Y_{total} = y₁ + y₂

Y_{total}= 22.90 + 21.20

Y_{total} = 44.1 m

we give the result in the form of module and angle

we use the Pythagorean theorem

R =
`\sqrt{X_(total)^2 + Y_(total)^2 }`

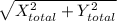
R =\sqrt58.6^2 + 44.1^2 }

R = 73.34 m

we use trigonometry

tan θ =

θ = tan⁻¹ \frac{ Y_{total} }{ X_{total} }

θ = tan⁻¹ \frac{ 44.1 }{ 58.6 } (44.1 / 58.6)

θ = -37º

this angle is in the second quadrant, given in the form of cardinal coordinates is

θ = 37º North of West