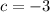Question

What is the value of c in this linear system? 5a - b + c = -10 a - 3b - c = -4 2a + 4b - 2c = 12 a) 2 b) 3 c) 1 d) -1

Answer 1

The correct value of c in the given linear system is −3 (option C).

The given system of equations is:

`\begin{aligned}5 a-b+c & =-10 \quad(\text { Equation 1) } \\a-3 b-c & =-4 \quad(\text { Equation 2) } \\2 a+4 b-2 c & =12 \quad(\text { Equation 3) }\end{aligned}`

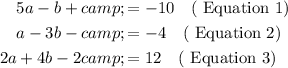
First, let's eliminate c from Equations 1 and 2 by adding them:

`(5 a-b+c)+(a-3 b-c)=-10+(-4)`

Simplifying, we get:

`6 a-4 b=-14 \quad(\text { Equation } 4)`

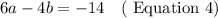
Next, let's eliminate c from Equations 1 and 3 by adding them:

`(5 a-b+c)+(2 a+4 b-2 c)=-10+12`

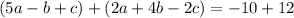
Simplifying, we get:

`7 a+3 b=2 \quad \text { (Equation 5) }`

Now, let's solve Equations 4 and 5 simultaneously. Multiply Equation 4 by 3 and Equation 5 by 2 to eliminate b:

`\left\{\begin{array}{l}18 a-12 b=-42 \\14 a+6 b=4\end{array}\right.`

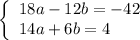
Adding these two equations:

`32 a=-38`

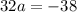
Dividing both sides by 32:

`a=-(19)/(16)`

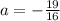
Now that we have the value of a, substitute it into Equation 5:

`7\left(-(19)/(16)\right)+3 b=2`

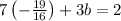
Solving for b:

`b=(17)/(16)`

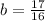
Finally, substitute the values of a and b into Equation 1 to solve for c:

`5 a-b+c=-10`

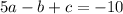
Substituting the values:

`5\left(-(19)/(16)\right)-(17)/(16)+c=-10`

Solving for c:

`c=-3`